การวิจัย

ข้อมูลกลุ่มวิจัยของภาควิชาคณิตศาสตร์

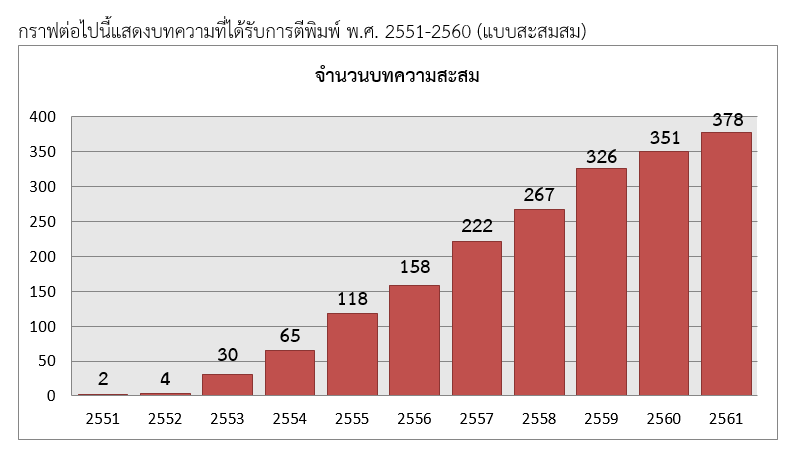
ภาควิชาคณิตศาสตร์ได้มีการจัดตั้งกลุ่มวิจัยเฉพาะด้านขึ้นมาเพื่อสร้างกลุ่มวิจัย และ สร้างนักศึกษาระดับบัณฑิตศึกษาให้มีศักยภาพในการแข่งขันด้านการวิจัย ได้แก่ กลุ่มวิจัยทฤษฎีจุดตรึง กลุ่มวิจัยทางพีชคณิต กลุ่มวิจัยฟังก์ชันวางนัยทั่วไป กลุ่มวิจัยทฤษฎีจำนวนและการประยุกต์ กลุ่มวิจัยทฤษฎีกราฟ กลุ่มวิจัยเชิงตัวเลขและการหาค่าเหมาะสมที่สุด กลุ่มวิจัยการเงินและการประกันภัย กลุ่มวิจัยทฤษฎีเสถียรภาพ และ กลุ่มวิจัยธรณีฟิสิกส์เชิงคำนวณ ทำให้จำนวนงานวิจัยของภาควิชาเพิ่มขึ้นอย่างต่อเนื่อง

กลุ่มวิจัยทฤษฎีจุดตรึง (Fixed Point Theory)

ทฤษฎีจุดตรึงเป็นการศึกษาเกี่ยวกับการมีอยู่จริง และระเบียบวิธีการประมาณค่าจุดตรึงของการส่งบางแบบ (fixed point of certain mapping) ภายใต้สมบัติบางประการ ทฤษฎีจุดตรึงมีบทบาทในหลากหลายสาขาวิชา เช่น สามการการเชิงอนุพันธ์และ เชิงปริพันธ์ (differential and integral equations) ทฤษฎีสมการเชิงฟังก์ชัน (theory of functional equations) ทฤษฎีเสถียรภาพ (stability theory) และ การหาค่าเหมาะสม (optimization)

กกลุ่มวิจัยทางพีชคณิต (Algebra)

เป็นการทราบกันดีแล้วว่าพีชคณิตเป็นแขนงหนึ่งทางคณิตศาสตร์ที่สำคัญ ที่มีผู้ศึกษามายาวนาน ดังตัวอย่างที่เห็นได้ชัดเจน คือ การหารากของสมการโพลีโนเมียลกำลังต่างๆ โดยความรู้เหล่านี้ท้ายที่สุดแล้วได้ถูกนำมาศึกษาในแบบนามธรรมยิ่งขึ้นกลายเป็นกลุ่มวิชาต่างๆ เช่น ทฤษฎีกรุป (group theory) ทฤษฎีริง (ring theory) และ ทฤษฎีฟีลด์ (field theory) ในกลุ่มวิจัยนี้ได้มุ่งเน้นความสนใจในด้านการศึกษาสมบัติทางพีชคณิตที่น่าสนใจของทฤษฎีกึ่งกลุ่ม (semigroup theory) และ ทฤษฎีกึ่งริง (semiring theory) ซึ่งทั้งสองทฤษฎีที่กล่าวมานี้ล้วนสามารถนำไปประยุกต์ใช้ในด้านวิศวกรรมศาสตร์รวมถึงในสาขาคอมพิวเตอร์อีกด้วย

กลุ่มวิจัยฟังก์ชันวางนัยทั่วไป (Generalized Functions)

กลุ่มวิจัยที่ศึกษาเกี่ยวกับทฤษฎีของฟังก์ชันวางนัย (generalized function) ฟังก์ชันพิเศษ (special function) สมการเชิงอนุพันธ์ (differential equation) สมการเชิงอนุพันธ์เศษส่วน (fractional differential equation) และ ควอนตัมแคลคูลัส (quantum calculus) รวมถึงการนำสิ่งที่ได้ศึกษาไปประยุกต์ใช้

กลุ่มวิจัยทฤษฎีจำนวนและการประยุกต์ (Number Theory and Applications)

ทฤษฎีจำนวนเป็นแขนงหนึ่งของคณิตศาสตร์ที่ศึกษาเกี่ยวกับสมบัติของจำนวนเต็มและสมบัติของจำนวนประเภทอื่นๆ ที่เป็นภาคขยายของจำนวนเต็ม เช่น จำนวนตรรกยะ จำนวนพีชคณิต เป็นต้น ในปัจจุบันได้มีการศึกษาทฤษฎีจำนวนโดยแบ่งย่อยออกไปตามเครื่องมือที่ใช้และสิ่งที่สนใจศึกษา เช่น ทฤษฎีจำนวนวิเคราะห์ (analytic number theory) ทฤษฎีจำนวนพีชคณิต (algebraic number theory) เรขาคณิตไดโอแฟนไทน์ (Diophantine geometry) เป็นต้น ซึ่งความรู้ด้านทฤษฎีจำนวนสามารถนำไปประยุกต์ใช้เป็นเครื่องมือสำคัญในศาสตร์แขนงอื่นๆ เช่น ทฤษฎีรหัส (coding theory) วิทยาการการเข้ารหัสลับ (Cryptography) และการสร้างจำนวนสุ่มเทียม (Pseudorandom numbers) เป็นต้น

กลุ่มวิจัยทฤษฎีกราฟ (Graph Theory)

ทฤษฎีกราฟเป็นสาขาวิชาทางคณิตศาสตร์ที่ศึกษากราฟซึ่งเป็นโครงสร้างที่แสดงความสัมพันธ์ระหว่างสิ่งต่างๆ โดยในส่วนของวิชาทฤษฎีกราฟมีทั้งทางการศึกษาทางทฤษฎีและการประยุกต์ใช้ที่แพร่หลายตั้งแต่ระดับพื้นฐานทั่วไป จนถึงระดับที่ต้องใช้ความรู้ขั้นสูง กลุ่มวิจัยนี้มุ่งเน้นในการศึกษาค้นคว้าทฤษฎี เพื่อให้ได้ค่าและคุณสมบัติทางกราฟที่น่าสนใจ โดยเฉพาะอย่างยิ่งในด้าน Graph Coloring ซึ่งเป็นการให้ค่าต่างๆ ในกราฟ ให้มีคุณสมบัติที่สอดคล้องกับเงื่อนไขที่กำหนด ซึ่งนอกจาก Graph Coloring จะมีคุณค่าในทางทฤษฎีเองแล้ว ยังถูกนำไปใช้งานเกี่ยวกับการจัดสรรทรัพยากร และการกำหนดช่วงเวลาที่เหมาะสมอีกด้วย

กลุ่มวิจัยเชิงตัวเลขและการหาค่าเหมาะสมที่สุด (Numerical Methods and Optimizations)

กลุ่มวิจัยนี้มีความสนใจด้านการวิเคราะห์และการออกแบบวิธีที่มีประสิทธิภาพซึ่งรวมไปถึงวิธีการเชิงเมตาฮิวริสติก วิธีเชิงประชากร วิธีเชิงสุ่ม วิธีเชิงสถิติ การศึกษาเชิงการทดลอง และการจำลองแบบ เพื่อนำไปประยุกต์ใช้กับปัญหาด้านต่างๆ ที่เกี่ยวข้องและทันสมัย เช่น ปัญหาการจัดตารางงาน ปัญหาการขนส่ง, AI, data science (big data), neural networks, digital processing เป็นต้น

กลุ่มวิจัยการเงินและการประกันภัย (Finance and Insurance)

ศึกษาค้นคว้าเกี่ยวกับทฤษฎีทางคณิตศาสตร์และสถิติ เพื่อนำไปประยุกต์ใช้เกี่ยวกับการประเมินความเสี่ยงทางการเงินและการประกันภัย รวมไปถึงการพยากรณ์ทางการเงินต่างๆ ซึ่งทำการวิเคราะห์ข้อมูลต่างๆ ในอดีตและปัจจุบันเพื่อนำมาประเมินความเสี่ยงที่จะเกิดขึ้นในอนาคตโดยมีการสร้างตัวแบบของเหตุการณ์การเสี่ยงภัยเป็นสำคัญ เพื่อประมาณและคาดการณ์และความเสี่ยงที่จะเกิดขึ้นให้มีความน่าจะเป็นไปได้ใกล้เคียงกับเหตุการณ์จริงมากที่สุด

กลุ่มวิจัยทฤษฎีเสถียรภาพ (Stability Theory)

มุ่งเน้นศึกษาทฤษฎีเสถียรภาพรูปแบบต่างๆ ของระบบพลศาสตร์ (dynamical system) ที่มีตัวหน่วงหลายๆ ระบบ เงื่อนไขของการมีเสถียรภาพของระบบต่างๆ ที่ได้มานั้น นอกจากจะเป็นทฤษฎีบทที่เป็นองค์ความรู้ใหม่แล้วยังสามารถนำไปต่อยอดความรู้ในทางคณิตศาสตร์ วิศวกรรมศาสตร์ การแพทย์ และสาขาอื่นๆ ได้

กลุ่มวิจัยธรณีฟิสิกส์เชิงคำนวณ (Computational Geophysics)

มุ่งเน้นสร้างงานวิจัยที่แก้ปัญหาที่เกี่ยวกับการสร้างแบบจำลองไปข้างหน้าทางธรณีฟิสิกส์ (geophysical forward modeling) ต่างๆ ด้วยการประยุกต์ใช้และดัดแปลงวิธีเชิงตัวเลขให้มีประสิทธิภาพและแม่นยำ นอกจากนี้ยังได้มุ่งเน้นการพัฒนาและสร้างงานวิจัยที่เกี่ยวกับการคำนวณย้อนกลับ (inversion) ที่ส่วนหนึ่งอาศัยกระบวนการแบบจำลองไปข้างหน้าที่พัฒนาขึ้นเพื่อนำไปใช้แปลความข้อมูลที่วัดได้จริงจากการสำรวจทางธรณีฟิสิกส์ต่างๆ ให้มีความแม่นยำ น่าเชื่อถือต่อการนำไปใช้เป็นเครื่องมือในการแปลความข้อมูลที่ได้จากการสำรวจทรัพยากรทางธรรมชาติต่างๆ